Fong & Spivak refer to category, functor, and natural transformation as the “big three” of category theory in their newly published textbook An Invitation to Applied Category Theory: Seven Sketches in Compositionality (henceforth Seven Sketches). In the previous seven posts of this series I’ve only written about categories. In this post I’m finally touching on functors.
The definition of a functor is straightforward. It’s just an arrow between two categories. Unlike arrows between objects (i.e., “arrows” when the word is used alone), functors map two types of data at once: objects and (inter-object) arrows. This is because at the functorial level the internal structures of the source and target categories are visible—recall that at the category-internal level the source and target objects are opaque.
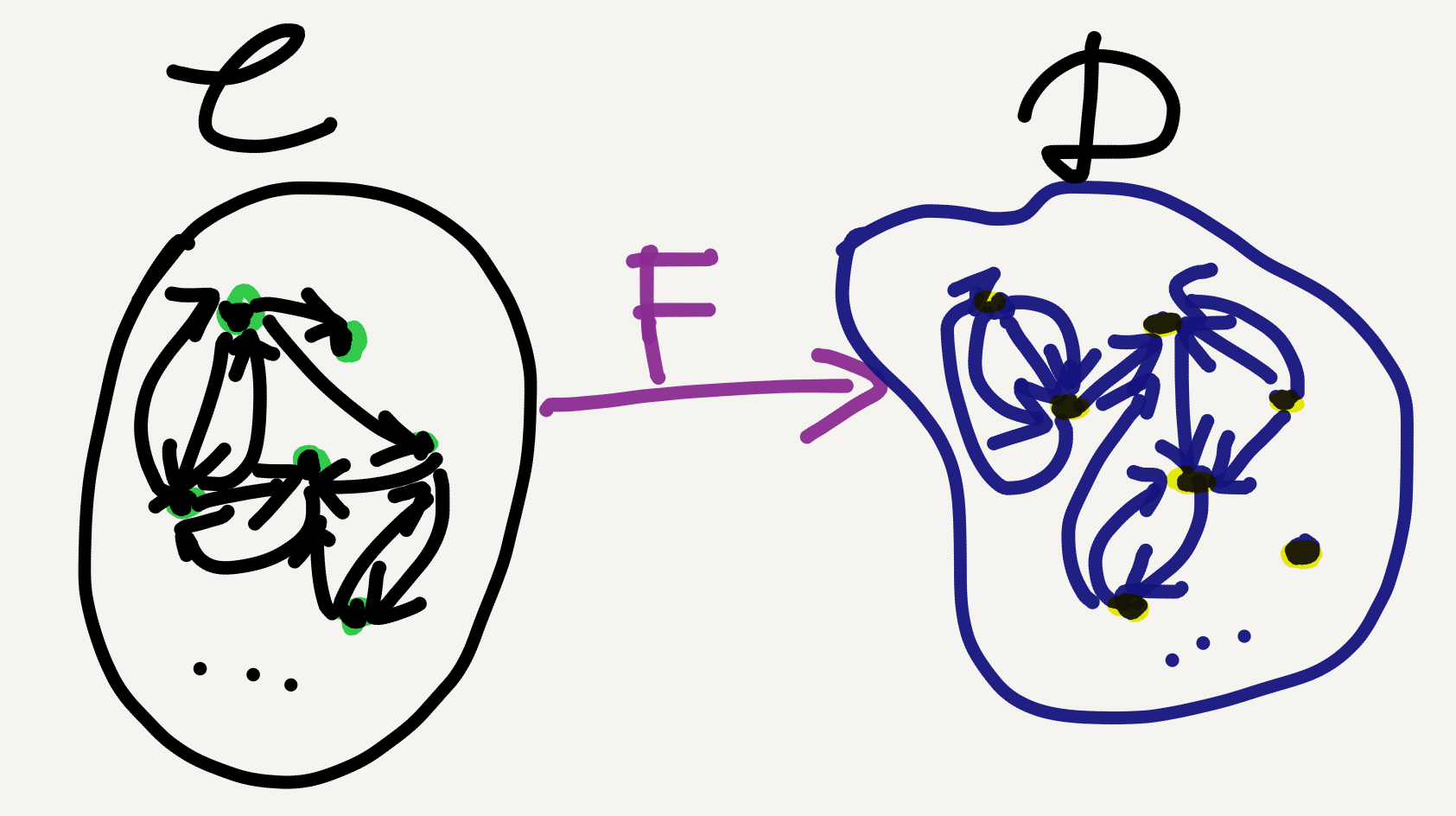
Functor defined
I mentioned the axiomatic definition of categories in my Aug 28 post. A category consists of a collection of objects and a collection of arrows (aka. morphisms), where each object is associated with an identity arrow and every pair of composable arrows actually compose, with the composition obeying associativity and the unit law. A functor maps all these data and their structures from one category to another. In Awodey’s words,
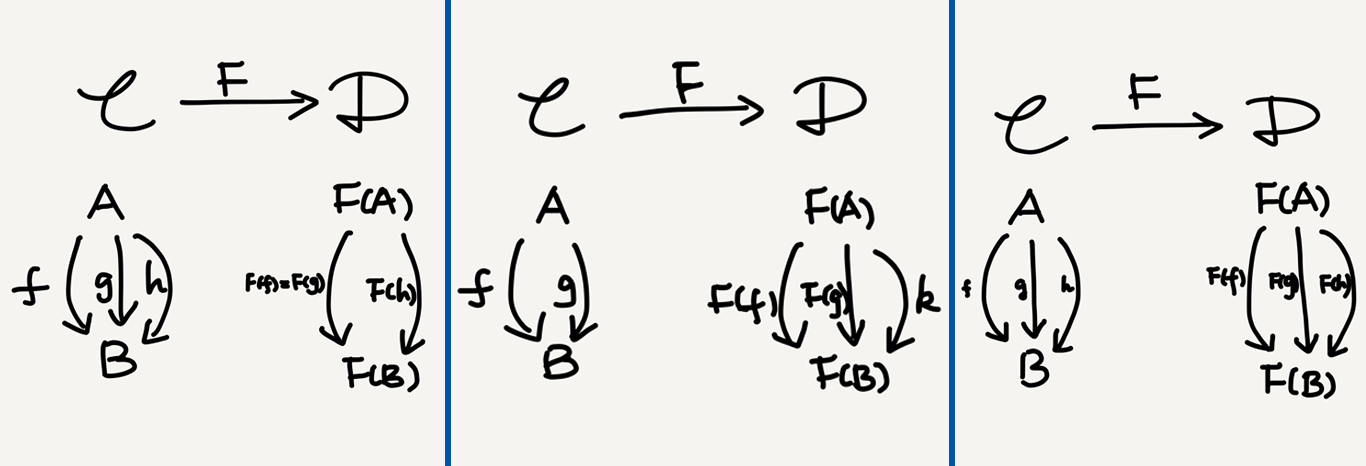
A functor $F\colon \mathbb{C}\rightarrow \mathbb{D}$ between categories $\mathbb{C}$ and $\mathbb{D}$ is a mapping of objects to objects and arrows to arrows, in such a way that
(a) $F(f\colon A\rightarrow B) = F(f)\colon F(A) \rightarrow F(B),$
(b) $ F(1_A) = 1_{F(A)}, $
(c) $F(g\circ f) = F(g)\circ F(f).$ (Category Theory, pp. 8–9)
So, a functor sort of creates an “image” of its source inside its target. Specifically, it may distort or collapse the source category but may not break connectivity.
A functor is two mappings
Functoriality is a highly compact notion. When we say $F\colon\mathbb{C}\rightarrow\mathbb{D}$ is a functor, we mean that $F$ maps all the above-specified data from $\mathbb{C}$ to $\mathbb{D}$. In other words, $F$ is not a single mapping but a “bundle” of mappings. In Mac Lane’s words:
[A] functor $T$ … consists of two suitably related functions: The object function $T$ … and the arrow function (also written $T$) …. (CWM, p. 13)
Mathematicians habitually write the object and the arrow functions both with the same letter (e.g., $T$). By contrast, the two functions have separate notations in some applied areas such as functional programming. Take Haskell for example. Its type class Functor is defined as follows:
class Functor f where
-- one method
fmap :: (a -> b) -> f a -> f b
-- two laws
fmap id == id
fmap (f . g) == fmap f . fmap g
As the definition shows, the Functor class in Haskell has a single method fmap that maps a function a -> b to another function f a -> f b, and this mapping must satisfy two laws: (i) it must preserve identity; (ii) it must preserve composition.
Comparing the definition of the Haskell Functor with that of the mathematical functor (see above), we can easily find that the two are essentially the same: fmap is just the arrow function, and f is the categorical object function. As such, the Haskell Functor class itself is merely half of a mathematical functor, while the other half is defined as a method of the class. For those who want to learn more about the categorical nature of Haskell I recommend Bartosz Milewski’s 2018 book Category Theory for Programmers.
Functor jectivity
Above I cited Mac Lane’s statement that a functor consists of two functions. An important property of function is jectivity: in set-theory a function can be injective (one-to-one), surjective (onto), or bijective (one-to-one correspondence).
The jectivity-based classification also makes sense in category theory—and at different abstraction levels. At the category-internal level, arrows are classified into monomorphisms, epimorphisms, and isomorphisms (see this blog post for an introduction); and at the functorial level, functors are classified as full, faithful, and so on. Here I won’t comment on arrow jectivity but will focus on functor jectivity, because I had only found the latter confusing.
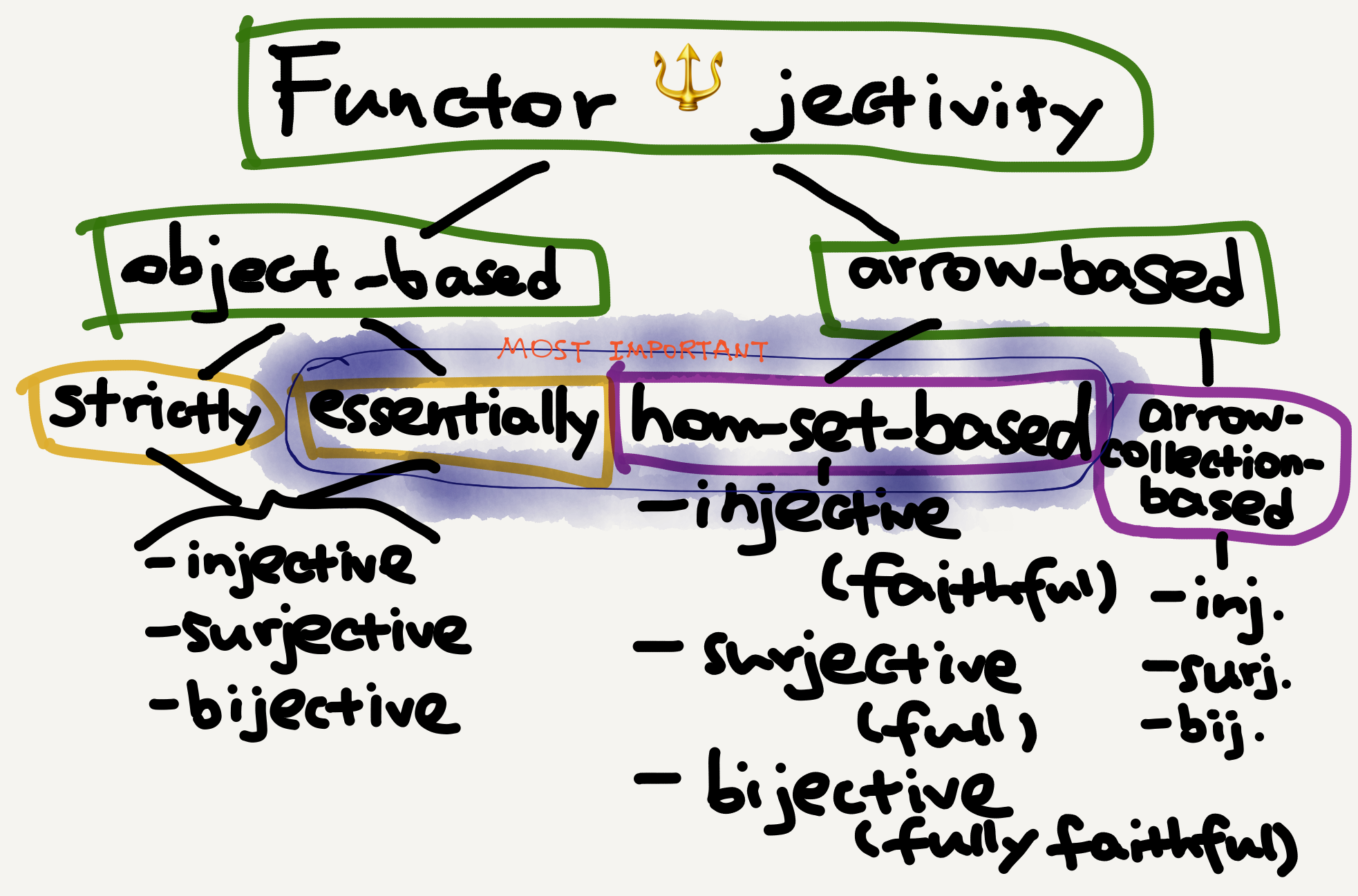
Since a functor consists of two functions, it can be given a jectivity class in two dimensions—one based on objects and the other based on arrows. Moreover, the arrow dimension further involves two subdimensions: that of the overall arrow collection of the category and that of the arrow collection between each pair of objects (i.e., the hom-set).
A note for beginners: Textbooks usually focus on the hom-set-based classification, which defines full, faithful, and fully faithful functors. However, since you sooner or later will encounter classifications in other (sub)dimensions, it’s better to learn the whole picture from the beginning so that you won’t experience unnecessary confusion like I did. As far as I know, Awodey’s textbook (p. 148) has the most complete introduction of the various jectivity classes for functors.
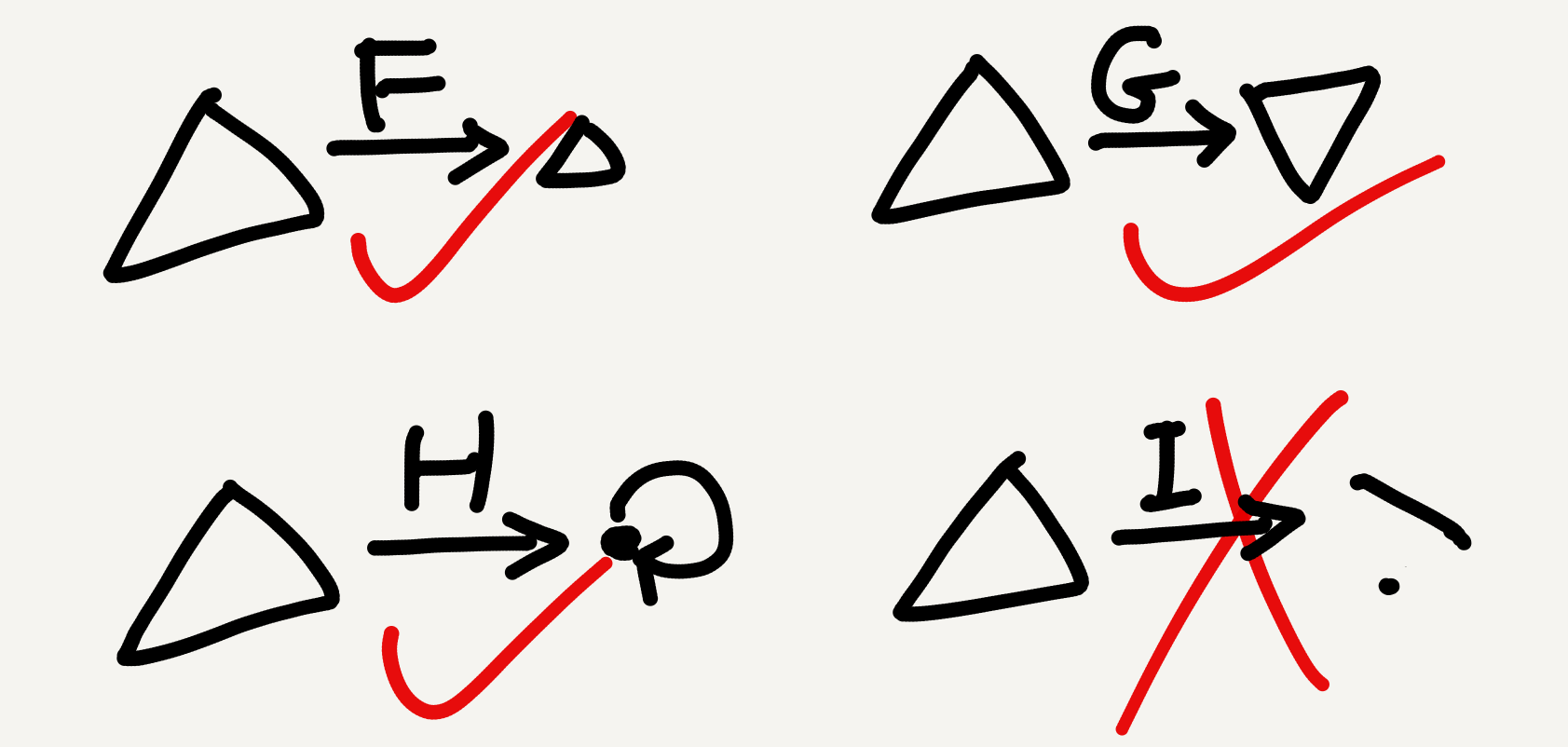
1. Jectivity based on hom-set
A functor is
- full if its hom-set mapping is surjective,
- faithful if its hom-set mapping is injective, and
- full and faithful (aka. fully faithful) if its hom-set mapping is bijective.
These full/faithful terms are widely taught mainly because they are closely related to another important categorical concept subcategory. A subcategory is related to its “supercategory” via an inclusion functor, which is automatically faithful (because the subcategory is just part of the supercategory) and in addition may also be full (when the “part” keeps hom-sets intact); in the latter case we have a full subcategory.
2. Jectivity based on object collection
A functor is
- injective on objects if its object function is injective,
- surjective on objects if its object function is surjective, and
- bijective on objects (aka. bo) if its object function is bijective.
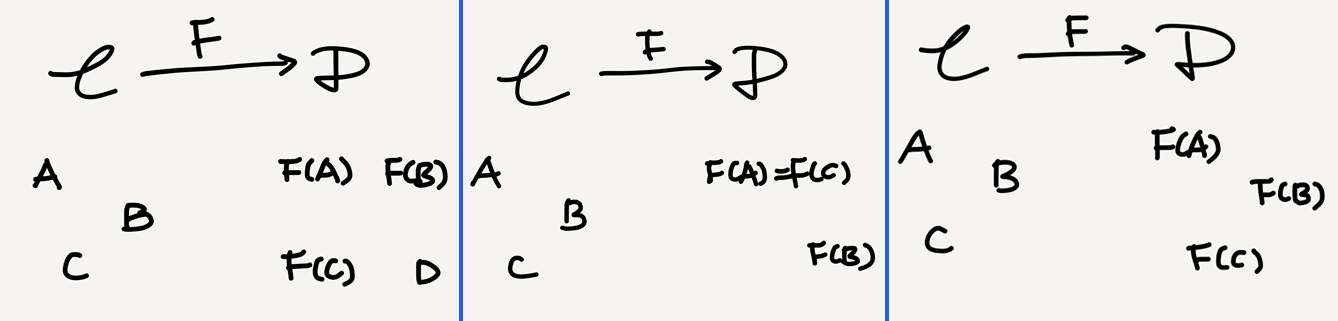
Taking isomorphic objects into account, we can also define the following “essentially” versions of the above terms—a functor is
- essentially injective on objects if its object function is injective up to isomorphism,
- essentially surjective on objects if its object function is surjective up to isomorphism, and
- essentially bijective on objects if its object function is bijective up to isomorphism.
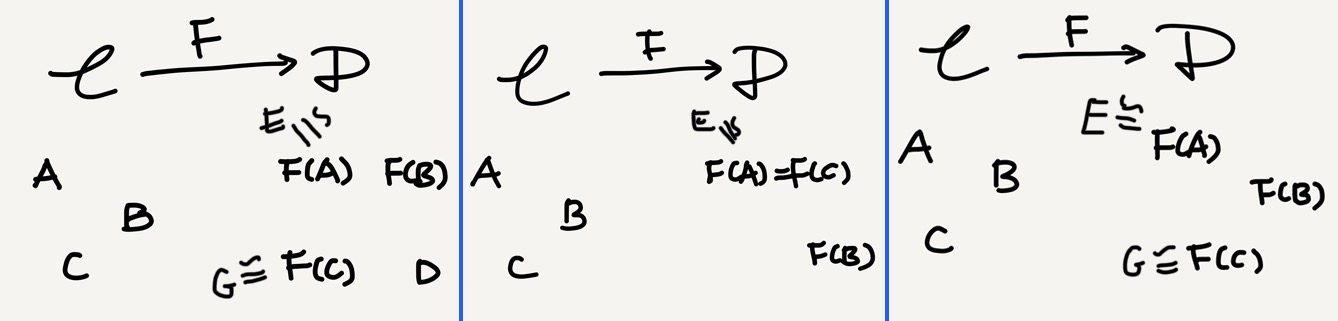
Two places I’ve seen these “essentially” notions1 are the definition of categorical embedding (full + faithful + essentially injective on objects) and that of categorical equivalence (full + faithful + essentially surjective on objects). I do have notes on both, but I’ll leave them to future posts.
3. Jectivity based on arrow collection
I haven’t met functor classes in this subdimension in my limited experience but list them anyway for completeness. A functor is
- injective on arrows if its arrow function is injective,
- surjective on arrows if its arrow function is surjective, and
- bijective on arrows if its arrow function is bijective.
I haven’t met any “essentially” versions of these terms either. In my experience when essentially injective/surjective/bijective is used alone the intended reading is always “… on objects.”
In sum, functor jectivity is a lot more complex than arrow jectivity, because a functor is really a bundle of mappings. I use the following picture to illustrate the above-mentioned classes:
Takeaway
- A functor consists of two suitably related functions, one on objects and the other on arrows.
- In Haskell the Functor type class merely corresponds to the object part of a categorical functor, while the arrow part is implemented as a method
fmapon the Functor class. - Functors can be classified based on jectivity in different (sub)dimensions, but the most useful subclasses for beginners to know are the hom-set-arrow-based “full/faithful” series and the isomorphism-supported-object-based “essentially” series.



Leave a comment