Category theory notes 10: Composite naturality (Part 1)

The notion of natural transformation is surprisingly easy to follow. If you know what an arrow is and what a functor is, then you automatically know what a natural transformation is—it’s just an arrow between functors. I actually wondered why in many textbooks the introduction of such a “natural” notion should wait till all the intervening complex stuff (e.g., universal properties) had been taught. If I were to write an introductory tutorial, I’d introduce functors and natural transformations immediately after categories (as Mac Lane does in CWM), since these are the “backbone” of category theory and to understand them we really don’t need to know too much else.

Naturality defined

There are three levels of arrow mapping in basic category theory:

• arrows between objects are morphisms ($f, g, h,$ etc.),
• arrows between categories are functors ($F, G, H,$ etc.), and
• arrows between functors are natural transformations ($\alpha, \beta, \gamma,$ etc.).

Three levels of arrow mapping in category theory: morphism (black), functor (red), and natural transformation (green)

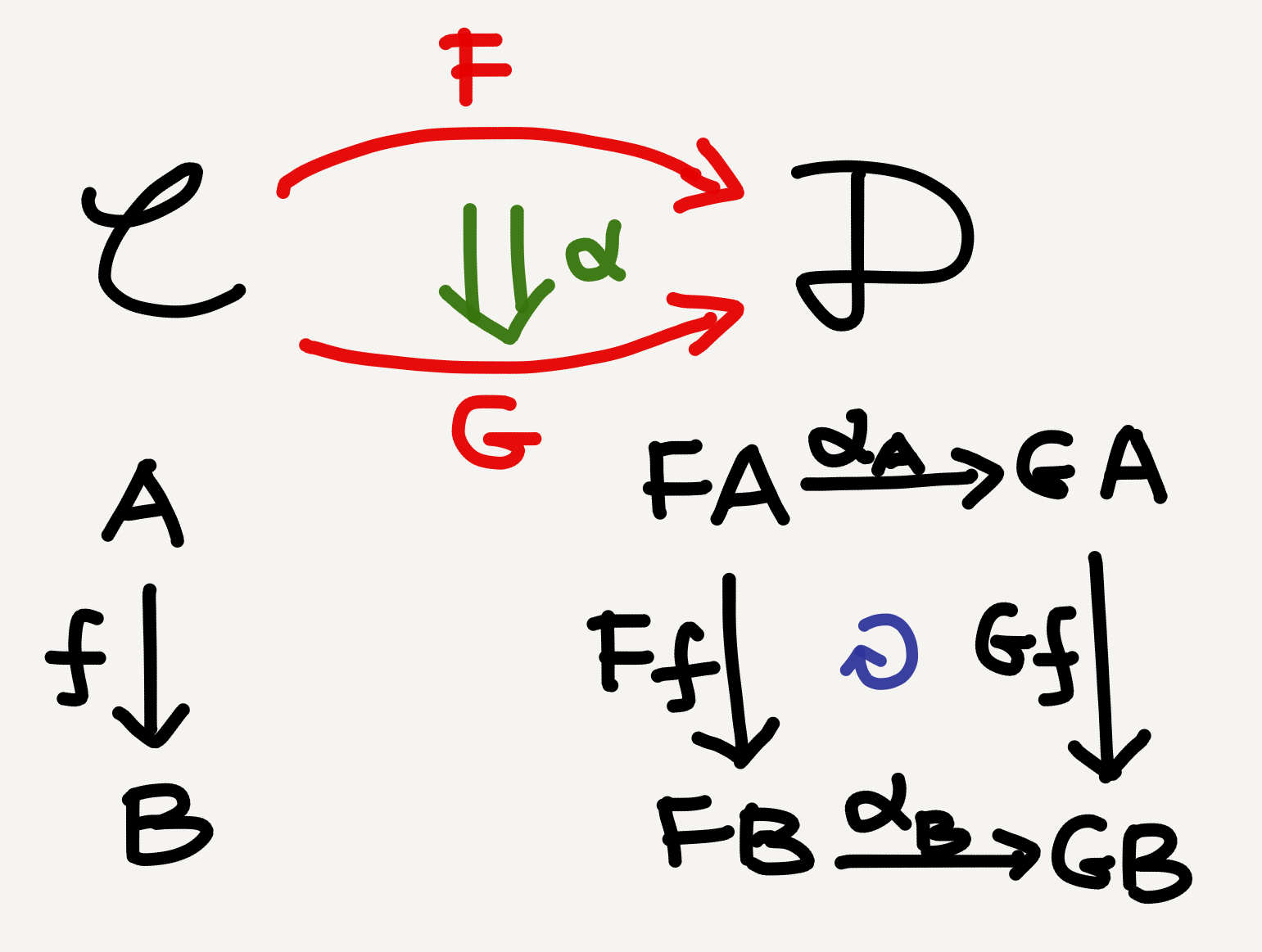
The formal definition of a natural transformation is as follows (from Wikipedia):

If $F$ and $G$ are functors between the categories $\mathbb{C}$ and $\mathbb{D},$ then a natural transformation $\eta$ from $F$ to $G$ is a family of morphisms that satisfies two requirements:

1. The natural transformation must associate to every object $X$ in $\mathbb{C}$ a morphism $\eta_X\colon F(X)\rightarrow G(X)$ between objects of $\mathbb{D}.$ The morphism $\eta_X$ is called the component of $\eta$ at $X.$

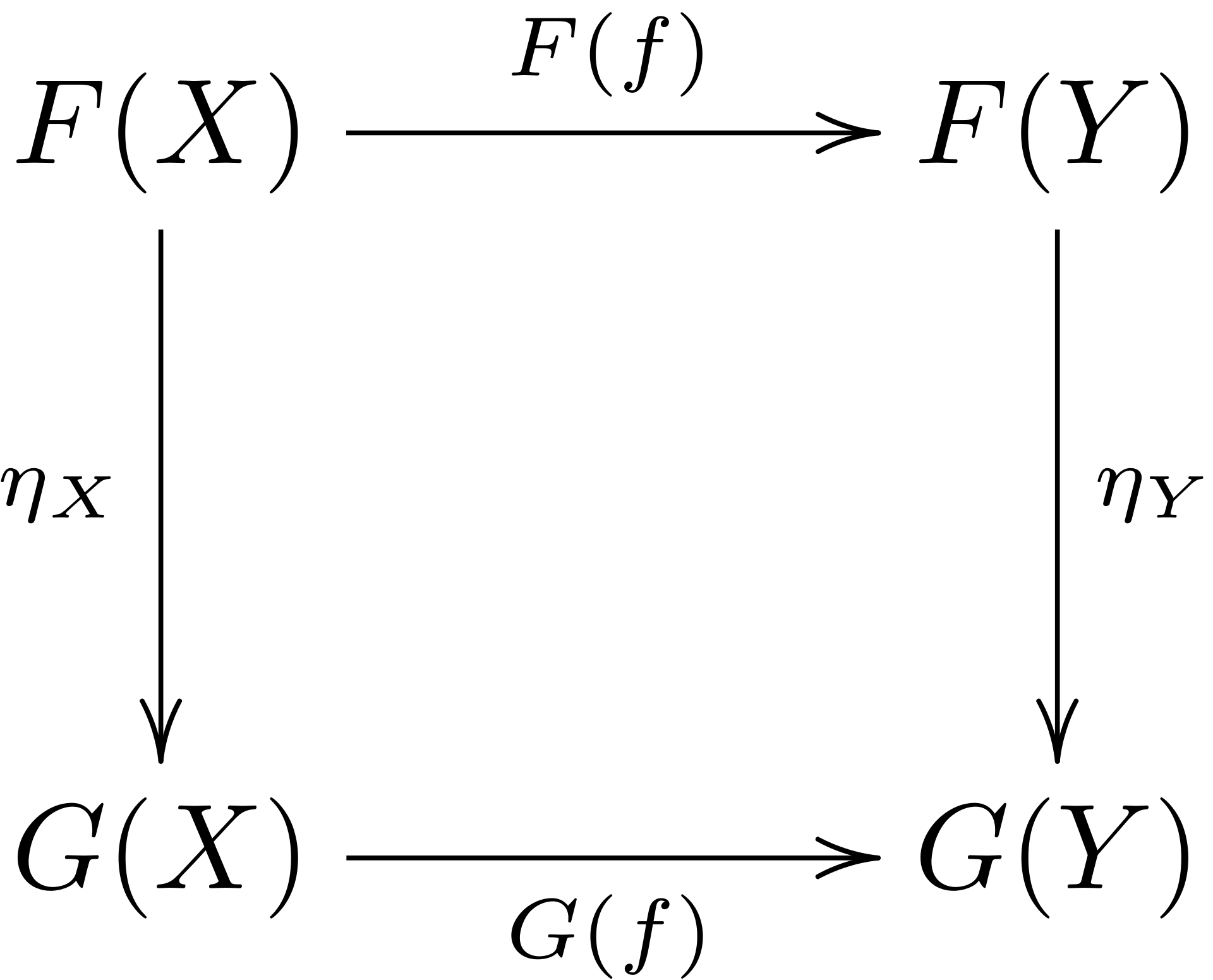
2. Components must be such that for every morphism $f\colon X\rightarrow Y$ in $\mathbb{C}$ we have $\eta_Y\circ F(f) = G(f)\circ\eta_X,$ diagrammatically

   

The above diagram is called a naturality square. In my hand-drawn picture above there’s also such a square, and I’ve explicitly indicated its commutativity with a round arrow (blue).

Vertical composition

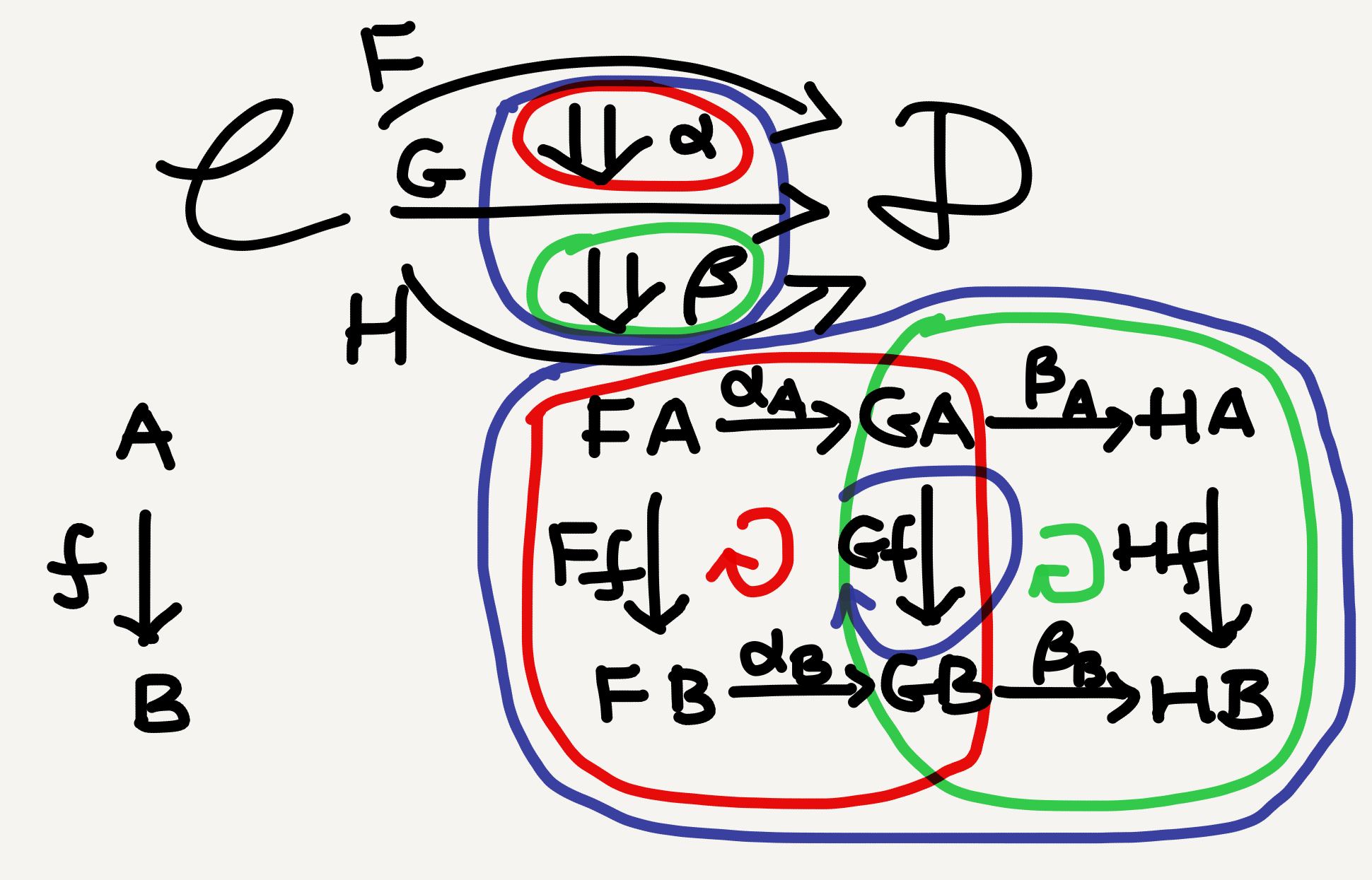
While natural transformations themselves are not difficult to understand, a point that I did find challenging was their composition. There are two ways to compose natural transformations: vertical composition ($\cdot$) and horizontal composition ($\circ$). Composing natural transformations vertically just means stacking them one above another to get a bigger natural transformation.

There are three natural transformations in the diagram above: $\alpha, \beta,$ and $\beta\cdot\alpha.$ The vertical composition of natural transformations is associative and unital: given three vertically stacked natural transformations $\alpha\colon F\Rightarrow G, \beta\colon G\Rightarrow H,$ and $\gamma\colon H\Rightarrow I$ (please imagine $I$ and $\gamma$ in your head), we have \[ \gamma\cdot(\beta\cdot\alpha) = (\gamma\cdot\beta)\cdot\alpha, \] \[ 1_G\cdot\alpha = \alpha,\; \text{and} \] \[ \beta\cdot 1_G = \beta, \] where $1_G$ is the identity natural transformation on $G.$ The associativity and unitality of natural transformation composition means all the functors between $\mathbb{C}$ and $\mathbb{D}$ together with all natural transformations between those functors form a category—a functor category.

What does the vertical composition of natural transformations mean for objects and morphisms? It’s just the side-by-side joining of two naturality squares, which yields a third and bigger naturality square, or more precisely rectangle.

Vertical composition joins two naturality squares side by side.

Horizontal composition

If the vertical composition of natural transformations is still easy to understand, their horizontal composition is much less intuitive (at least for me). Horizontal composition refers to the composition of two side-by-side natural transformations in a configuration like

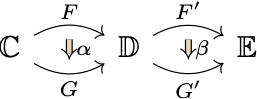
Here the intended composition is $\beta\circ\alpha.$ But how is this composition possible? The target of $\alpha$ (i.e., $G$) and the source of $\beta$ (i.e., $F^\prime$) don’t overlap after all!

It took me quite some time to get used to this, but the so-called horizontal composition is not really composition in the ordinary sense—it’s composition in a higher category (a 2-category) instead. Higher categories are quite fashionable among categorists. If you go to nLab you’ll find that almost every page mentions it…😝 But since we are nonmathematician beginners, we don’t want to dive into higher category theory immediately and feel like idiots there. The good news is that the horizontal composition of natural transformations can be perfectly expressed in ordinary (i.e., 1-category) terms. (But if you want a peek into the 2-category perspective, I recommend Milewski’s Category Theory for Programmers, §10.4.)

Long story short, the “composition” of $\alpha\colon F\Rightarrow G$ and $\beta\colon F^\prime\Rightarrow G^\prime$ in the above diagram is essentially a natural transformation between the two composite functors $F^\prime\circ F$ and $G^\prime\circ G,$ diagrammatically

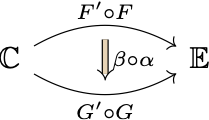
And this bigger natural transformation is called a “composition of $\alpha$ and $\beta$” simply because it can be expressed (and hence determined) by $\alpha$ and $\beta.$ To see how, let’s draw a picture.

Horizontal composition “lifts the dimension of” objects and morphisms.

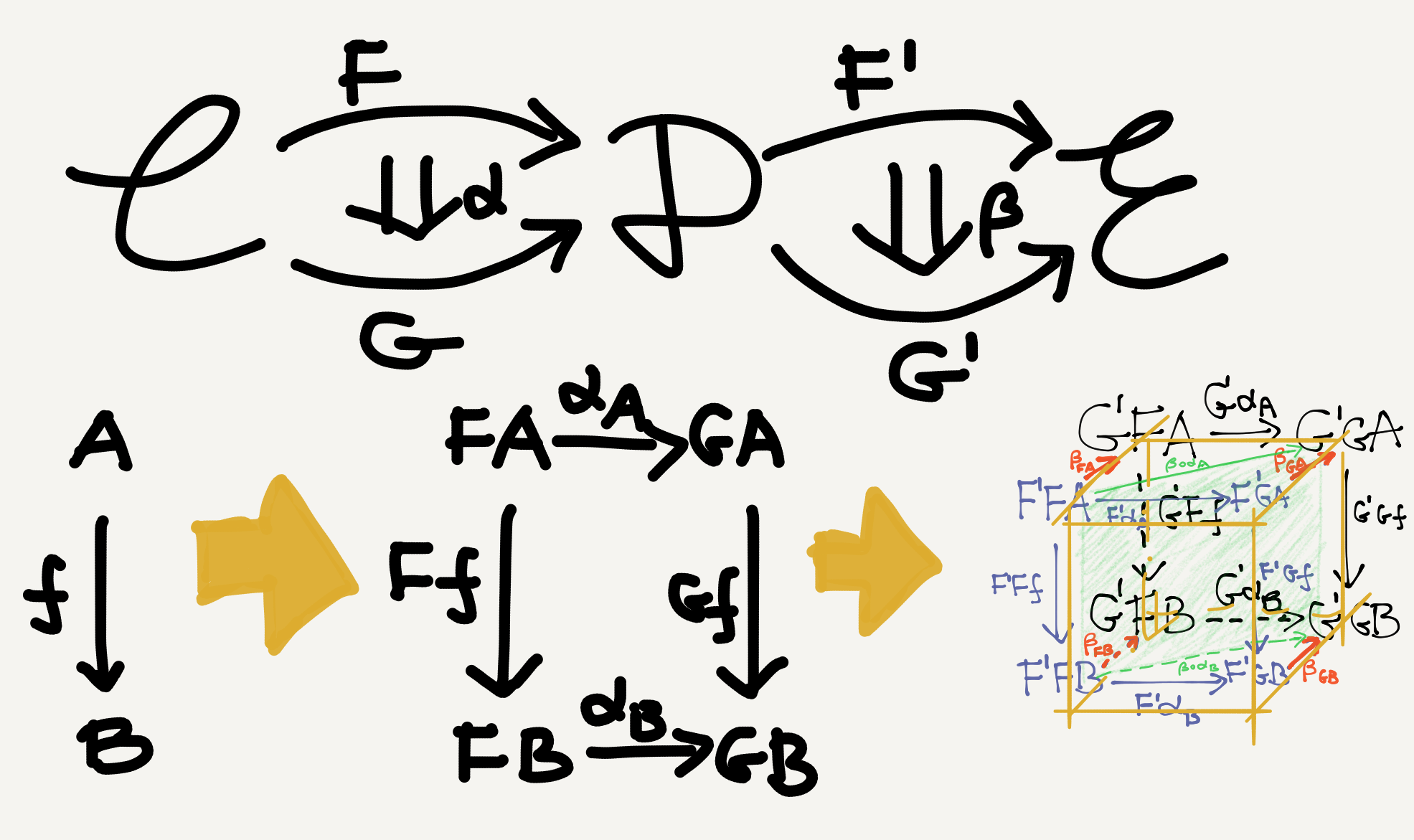
In the above picture, the effect of the consecutive application of the two natural transformations $\alpha$ and $\beta$ on the $\mathbb{C}$-morphism $f\colon A\rightarrow B$ is sort of like dimension lifting—an edge in $\mathbb{C}$ becomes a face in $\mathbb{D}$ and a cube in $\mathbb{E}.$ This is the case because each functor (e.g., $F$) maps a morphism to a morphism and each pair of natural transformation components (e.g., $\alpha_A,\alpha_B$) connect two such morphisms into a square. And since natural transformation components themselves are also morphisms, they also get mapped by further functors and connected by further natural transformations.

Thus, the naturality square in $\mathbb{D}$ is mapped twice into $\mathbb{E},$ once by $F^\prime$ and once by $G^\prime,$ which are the front and back faces of a cube. The remaining four faces of the cube are formed by natural transformation components (orange). Once we have this cube, we can easily see that it has a rectangular cross section $F^\prime FA - F^\prime FB - G^\prime GB - G^\prime GA$ (green). The nice thing about this cross section is that its four vertices can be viewed as $A$ and $B$ lifted by the two composite functors $F^\prime F$ and $G^\prime G$: \[ F^\prime FA - F^\prime FB - G^\prime GB - G^\prime GA = (F^\prime\circ F)A - (F^\prime\circ F)B - (G^\prime\circ G)B - (G^\prime\circ G)A. \] Similarly, the two vertical edges $F^\prime FA - F^\prime FB$ and $G^\prime GA - G^\prime GB$ can be viewed as the functorial lifting of the $\mathbb{C}$-morphism $f\colon A\rightarrow B.$ The two horizontal edges $F^\prime FA - G^\prime GA$ and $F^\prime FB - G^\prime GB,$ on the other hand, are just two components of the composite natural transformation $\beta\circ\alpha.$

In other words, the green cross section above is precisely the naturality square for $\beta\circ\alpha.$ Letting $\langle A,B,f\rangle$ vary in $\mathbb{C},$ we get a family of such cross section squares, which demonstrates the naturality of $\beta\circ\alpha.$

The natural in natural transformation simply means that naturality squares always commute whichever objects and morphisms in the source category we choose to map.

Just like vertical composition, horizontal composition is also associative and unital: \[ \gamma\circ(\beta\circ\alpha) = (\gamma\circ\beta)\circ\alpha \] \[ 1_{id_\mathbb{D}}\circ\alpha = \alpha \] \[ \beta\circ1_{id_\mathbb{D}} = \beta\] Here $1_{id_\mathbb{D}}$ is the identity natural transformation on the identity functor on the category $\mathbb{D}.$ 😝

For the remaining part of this article see my next post “Category theory notes 11: Composite naturality (Part 2).”