Category theory notes 11: Composite naturality (Part 2)

In my previous post “Category theory notes 10: Composite naturality (Part 1)” I illustrated the vertical and horizontal compositions of natural transformations. In this post I continue to comment on natural transformation composition.

Relationship between horizontal and vertical identities

The identities for vertical and horizontal natural transformation composition are closely related to each other. In Mac Lane’s words:

[T]he identity for the [horizontal] composition $\circ$ … is also the identity for the [vertical] composition $\cdot.$
The collection of all natural transformations is the set of arrows [between] two different categories under two different operations of composition, $\cdot$ and $\circ$ … any arrow (transformation) which is an identity for the composition $\circ$ is also an identity for the composition $\cdot.$ (CWM, p. 43)

Milewski also states (presumably following Mac Lane):

[T]he identity for horizontal composition is also the identity for vertical composition, but not vice versa. (Category Theory for Programmers, p. 175)

This association seems to be an important facet of natural transformation composition as well as a basic characteristic of 2-categories:

A 2-category (short for two-dimensional category) is a double category in which every identity arrow for the first [i.e., horizontal] composition is also an identity for the second [i.e., vertical] composition. (CWM, p. 44)

Unfortunately I didn’t find any further explanation in textbooks or online. When the relationship between the horizontal and the vertical composition identities is mentioned, it’s always mentioned in passing and basically a repetition of Mac Lane’s words. So I can only guess what it really means based on my own understanding. The following are just my own tentative thoughts and not necessarily correct. If you know the correct answer please leave a comment!

1. The identities of horizontal and vertical compositions of natural transformations are both natural transformations themselves; that’s the background basis for their correlation, because if the two identities are different kinds of constructs there’s no reason to identify them.
2. A horizontal identity is simultaneously a vertical identity because all identity natural transformations are automatically vertical identities and a horizontal identity is an identity natural transformation too.

3. Nevertheless, a horizontal identity is not just any identity natural transformation but a very special one—it’s the identity natural transformation on an identity functor! Thus, it’s only the vertical identity of natural transformations between endofunctors, say all functors from $\mathbb{C}$ to itself, but not that of natural transformations between other parallel functors, say functors from $\mathbb{C}$ to $\mathbb{D}.$

   In other words, the class of vertical identities is much larger than the class of horizontal identities. Therefore, that something is in the former class doesn’t guarantee that it’s also in the latter, whereas if something is in the latter class then it must also be in the former. This is probably what Milewski means by “not vice versa.”

   

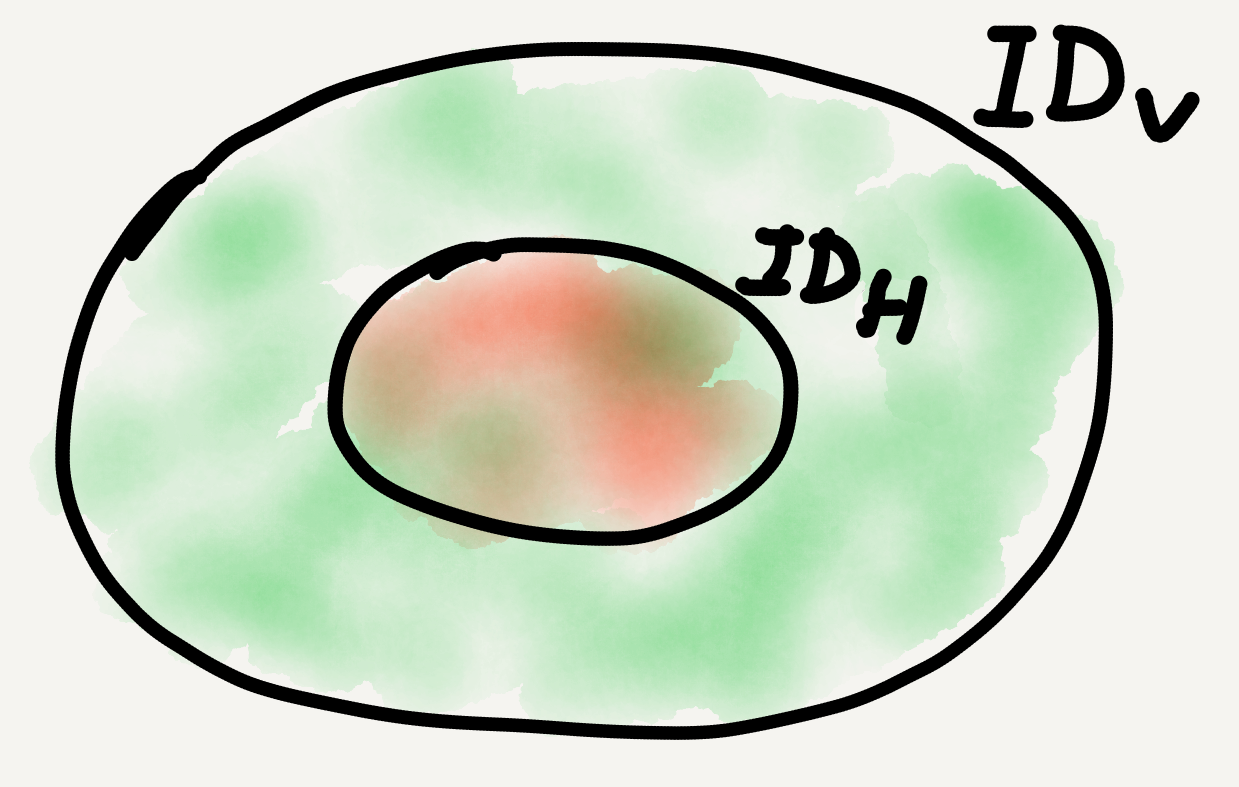
   The class $ID_H$ of horizontal identities is a proper subclass of the class $ID_V$ of vertical identities of natural transformation composition.

Interchange law

Anyway, even if we don’t fully understand the relationship between horizontal and vertical identities, we can still successfully understand another important correlation between the two ways to compose natural transformations—the interchange law. The law says that in the following configuration, where $\mathbb{C}, \mathbb{D}, \mathbb{E}$ are categories, $F, F’,$ etc. are functors, and $\alpha, \alpha’,$ etc. are natural transformations,

we get the same composite natural transformation whichever way we choose to do the composition; that is, either vertically before horizontally or horizontally before vertically. In formal notation: \[ (\beta^\prime\cdot\alpha^\prime)\circ(\beta\cdot\alpha) = (\beta^\prime\circ\beta)\cdot(\alpha^\prime\circ\alpha). \] Since vertical composition produces squares and horizontal composition produces cubes (that is, in their first applications), the overall diagram of the four-natural-transformation composition should be four cubes joined side by side, and one of the rectangular cross sections of the big cuboid should be the composite naturality square we need. This picture is tricky to draw but below is my attempt (I’ve omitted some morphism labels to reduce clutter):

The interchange law of natural transformation composition

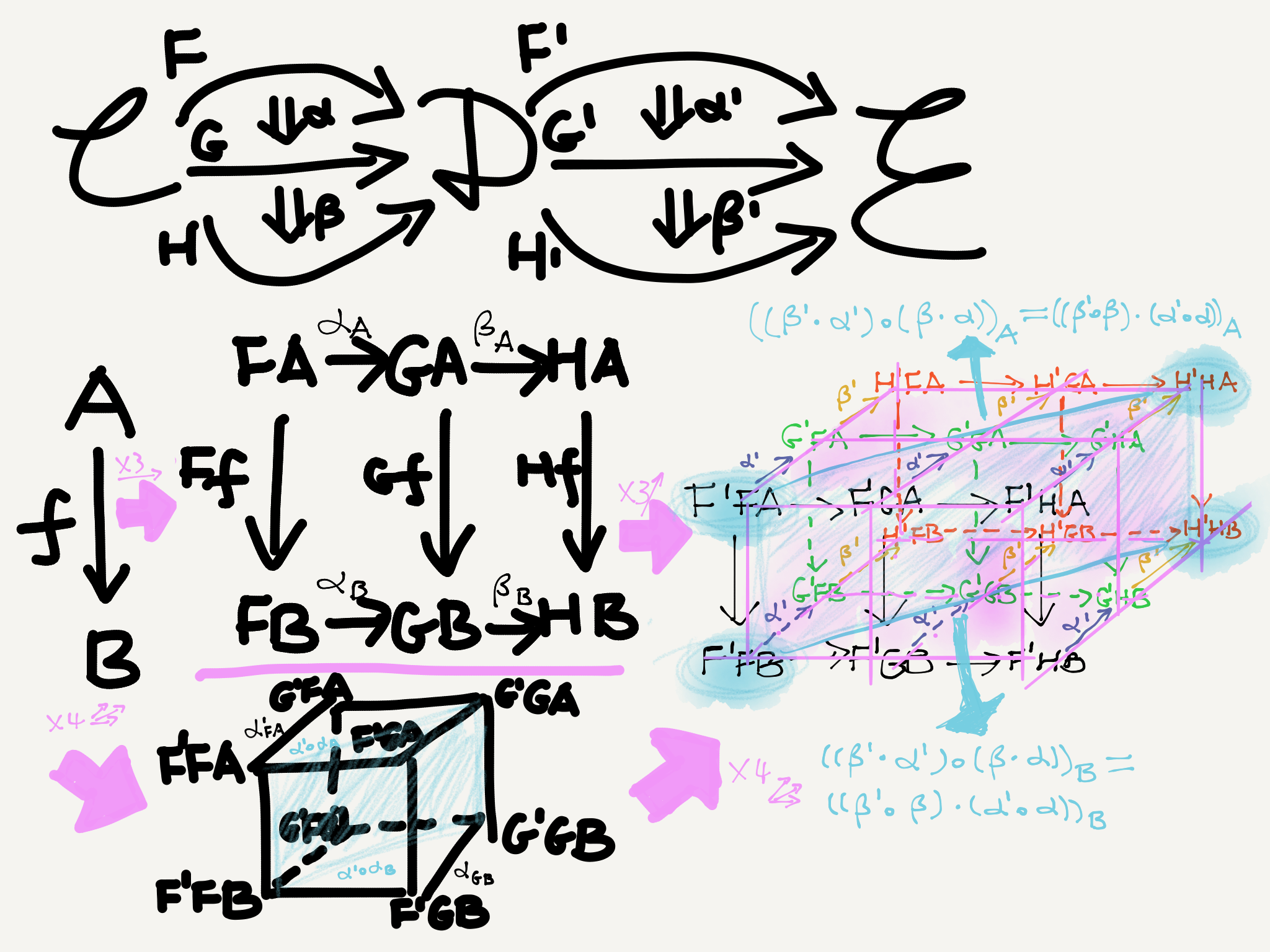
As the picture shows, the interchange law essentially describes two ways to get a four-cube cuboid from a single edge: either via the “proliferation” of a two-square rectangle or via that of a single cube.

• On the one hand, we can first copy the edge $A\rightarrow B$ rightward three times, thus forming a rectangle, and then copy the rectangle backward three times.
• On the other hand, we can first copy the edge $A\rightarrow B$ once in all three directions (rightward, backward, and diagonally to the right/back), thus forming a cube, and then copy the cube once in all three directions again.

Either way, we end up with a $2\times2\times1$ cuboid whose cross section $F’FA - F’FB - H’HB - H’HA$ (blue) is the composite naturality square we want. The square describes a composite natural transformation between the composite functors $F’F$ and $H’H.$

Takeaway

• Natural transformations are arrows between functors.
• Natural transformations can be composed vertically or horizontally, and both forms of composition are associative and unital.
• An identity natural transformation for horizontal composition is also an identity for vertical composition but not vice versa.
• The vertical and horizontal composition of natural transformations can be integrated via the interchange law.