Category theory notes 9: Full and half inverses

Category theory textbooks often warn learners that categorical objects and arrows shouldn’t be tied to sets and functions. A poset category, for example, has elements¹ as objects and instances of a binary relation as arrows.

The objects and arrows in a poset category aren’t sets and functions.

That being said, it’s undeniable that set theory has provided much inspiration for category theory, as reflected in the latter’s terminology. For example, each categorical arrow has a source (aka domain) and a target (aka codomain), just like a function; and arrow composition in a category is also very much like function composition—even its usual small circle notation (e.g., $g\circ f$) is a function-based convention (introduced by followers of Leibniz).

Inverse

The topic of this post, inverse, has a set-theoretic origin too. The following definition is from Wikipedia:

Let $f$ be a function whose domain is the set $X,$ and whose image (range) is the set $Y.$ Then $f$ is invertible if there exists a function $g$ with domain $Y$ and image $X,$ with the property $f(x)=y \Leftrightarrow g(y)=x.$ If $f$ is invertible, the function $g$ is unique, … called the inverse of $f$ [and] usually denoted as $f^{-1}.$

The category-theoretic definition of inverse is similar, as follows:

An inverse of a morphism $f\colon X\rightarrow Y$ in a category … is another morphism $f^{-1}\colon Y\rightarrow X$ which is both a left-inverse (a retraction) as well as a right-inverse (a section) of $f$, in that $f\circ f^{-1}\colon Y\rightarrow Y$ equals the identity morphism on $Y$ and $f^{-1}\circ f\colon X\rightarrow X$ equals the identity morphism on $X.$ (nLab)

In particular, an inverse is also called an isomorphism in category theory, though isomorphism is a broader concept. When $a$ and $b$ are isomorphic to each other, they are literally the same from a categorical perspective (hence the esoteric idiom “up to isomorphism”; see my Aug 31 post). To illustrate, if I take the bus to school, the “I” in the bus and the “I” at school are obviously the same person. More precisely, even though “we” are not completely identical given environmental and biological changes (e.g., my cells keep updating and my thoughts are dynamic too), “we” can be treated as the same person in all but the highly philosophical contexts; hence, Me-in-Bus $\cong$ Me-at-School ($\cong$ is the symbol for isomorphism).

An isomorphism is a full (i.e., two-sided) inverse.

Half inverses

Perhaps because the notion of isomorphism, or full inverse, is too strict, mathematicians have invented two half inverses as mentioned above. Starting with a full inverse

$,$

take either of its two equations, say $f\circ g = 1_Y$, and discard the other (here $g\circ f=1_X$), and we obtain a half inverse. In this situation, $f$ is called a left inverse of $g$ because it’s on the left of the small circle $\circ$, and $g$ is said to be a right inverse of $f$ because it’s on the right of $\circ$.

I must admit that these half-inverse notions gave me a real headache in the beginning, not because of their conceptual complexity—they aren’t that complex—but because of their names. The two half inverses each have three alternative names!

• left inverse and right inverse
• section and retraction
• split monomorphism and split epimorphism

I found these terms bewildering for three reasons.

1. I had to pay extra attention to the reference point of left and right

In particular, there are two legitimate reference points for left and right in category theory: a syntactic one and a diagrammatic one.

• Syntactically, given an equation like $f\circ g=1_Y,$ we just treat this expression as a string of symbols without considering its meaning; $f$ is left just because it’s literally on the left!

• Diagrammatically, given the same equation we can draw a commutative diagram

  

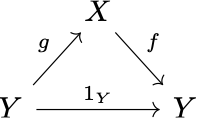
  where the intuitive reference point is the geometrical center of the shape; but now $g$ becomes on the left and $f$ on the right!

Apparently the inventors of the terms “left/right inverse” have used the syntactic reference point, as is the case with most left/right terms in category theory (e.g., left/right-cancelable, left/right adjoint), but since this choice is more arbitrary than principled, and considering syntactic thinking is much less intuitive than diagrammatic thinking in category theory, it makes the two half-inverse concepts harder to grasp than necessary for beginners.

2. I didn’t know why the terms section and retraction had been chosen

And I still don’t know why today. The terms may well have been borrowed from other mathematical areas, but without a note on their etymology few nonmathematician learners can see the motivation for choosing these names. In my case I had to memorize them by rote, and the diagrammatic visualization helped a lot—I just associated section with the left-hand arrow and retraction with the right-hand arrow in the diagram

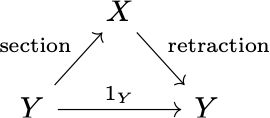
though obviously this added to the difficulty of remembering the “left/right inverses”… because the left-hand arrow is the right inverse!😓

So if you decide to use “section” and “retraction” (like me), then it’s better to temporarily forget “left inverse” and “right inverse” until you’re familiar enough with the subject not to mix its deliberately confusing lefts and rights.

3. I didn’t know what split meant or even its part of speech

At first I had thought split was the past participle of the verb split, as is usually the case when split is used as an attributive modifier (e.g., split bamboo).

A split bamboo floor (source: Wikimedia Commons, by Greg Willis)

If this were true, however, a split monomorphism would mean “a monomorphism that is split in two,” which is nonsensical, as there’s nothing like half a monomorphism in category theory. But if split is not a past-participle modifier, what else can it be? I couldn’t think of any possibility that would yield a reasonable meaning for the phrase split monomorphism. Later I saw the word split being used in a few other places under the same topic (i.e., half inverses):

…all idempotent can split in this way [i.e., into a section-retraction pair]… (Lawvere & Schanuel 2009, Conceptual Mathematics, p. 54)

…the pair $(r,m)$ [$r$ is a retraction of $m$ and $m$ is a section of $r$] is a splitting of the idempotent $m\circ r\colon B\rightarrow B.$ (nLab)

In this situation [i.e., $id\colon A\xrightarrow{i} B\xrightarrow{r}A$] $r$ is a split epimorphism and $i$ is a split monomorphism. The entire situation is said to be a splitting of the idempotent $B\xrightarrow{r}A\xrightarrow{i}B.$ (nLab)

A split mono (epi) is an arrow with a left (right) inverse. Given arrows $e\colon X\rightarrow A$ and $s\colon A\rightarrow X$ such that $es=1_A,$ the arrow $s$ is called a section or splitting of $e,$ and the arrow $e$ is called a retraction of $s$. … In $\mathbf{Sets}$, every mono splits except those of the form $\emptyset\rightarrowtail A$. The condition that every epi splits is the categorical version of the axiom of choice. (Awodey 2010, p. 32)

The word split is used in two difference ways in the above four quotes. In Lawvere & Schanuel’s textbook (which I highly recommend for the half-inverse-related notions) and in the nLab definitions split is used as an intransitive verb whose subject is an idempotent map. Thus we can say

• An idempotent map splits into a section and a retraction. and
• A section-retraction pair together form a splitting of an idempotent map.

In the second sentence above split is nominalized but its logical subject is still the idempotent map. Basically an idempotent map here is just the section and retraction maps composed in the other direction; that is, $\text{section}\circ\text{retraction}$ in the following diagram:

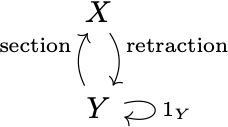
The idempotent map doesn’t equal $1_X$ but has another nice property: \[ \text{section}\circ\text{retraction}\circ(\text{section}\circ\text{retraction})=\text{section}\circ\text{retraction}. \]

By comparison, Awodey (2010) uses split as a transitive verb whose subject and object are respectively a section and a retraction (or vice versa). That is, Awodey lets the section and the retraction split each other!

Between the above two different usages of split, I think the idempotent-map-based one is more coherent, at least with regard to itself, because the idempotent map is indeed split into two parts—a section and a retraction. Awodey’s usage of split doesn’t sound coherent because it again suggests that the monomorphism/epimorphism is split in half (i.e., split in split mono/epi is a past-participle modifier), but there are no half monomorphisms/epimorphisms in category theory as I mentioned above; so there’s no reason to split them.

Anyway, the phrases split monomorphism and split epimorphism don’t make much sense grammatically. Even under the idempotent-map-based usage we still can’t assign split an appropriate part of speech, and the two terms can only be defined by force and learned by rote.

Use section/retraction

If you’ve been following my blog, you should have noticed that I’m more easily confused by names of things than by their essence. I’m not sure if it’s just me or a common feeling shared by others, but I tend to feel quite helpless and even dismayed when faced with a non-self-explanatory term in an introductory textbook without a clear note on why it’s chosen. And I felt even worse in the case of the half-inverse terms because they were not only opaque but also freely alternating—why using three interchangeable terms in parallel when one would do?!

That’s a question I haven’t found an answer to till today, and I’ve given up finding out why after getting accustomed to the opaque names, though I do try to stick to the most opaque yet least ambiguous section/retraction in my own writing—perhaps their nonambiguity is precisely thanks to their utter opaqueness. At least in this way I’m not bothered by the confusing left/right-handedness or the mystical grammatical abstruseness of split…

Takeaway

• In category theory a full or two-sided inverse is an isomorphism.
• A full inverse can be divided into two half inverses, which can exist without each other.
• The half inverses each have three alternative names, among which I think section and retraction are the least confusing.

---

1.^↩ Of course, these elements can be sets (e.g., in a powerset-based poset), but the point is that they needn't be.